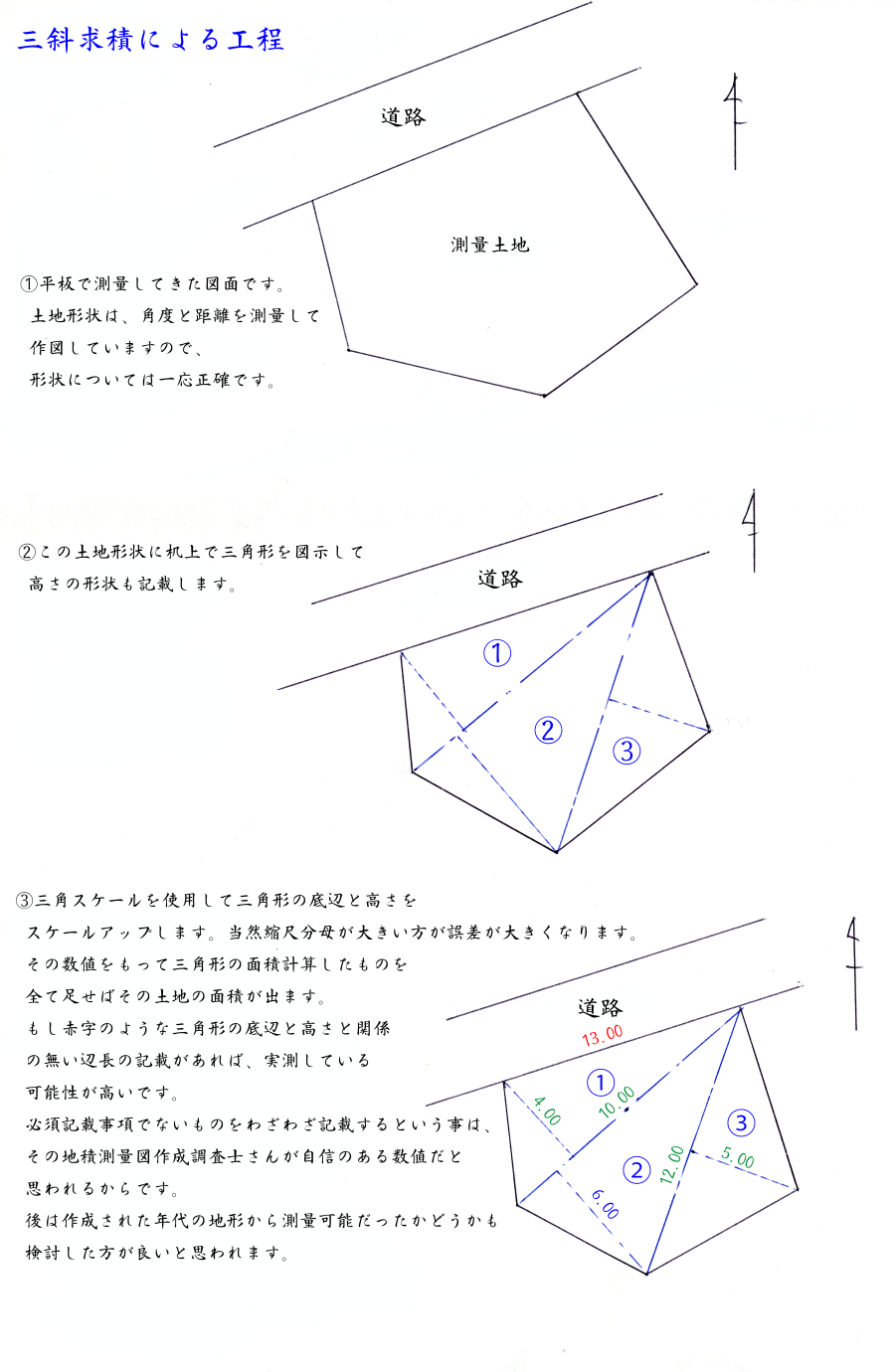
三斜法による求積とは、求積したい土地をいくつかの三角形に分けて、個々の三角形について求積をして
最後に三角形の面積を足して求積する方法です。三角形は当然、「底辺×高さ÷2」で計算します。
斜めの辺が3本あるから三斜というのではないでしょうか。
現在は座標で土地の面積は求積しますので、昔の計算方法ですが、今でもお客様が理解し易いので、あえて
この方法を取るケースもあります。弱点は、原則として土地の底辺と高さだけの表示となりますので、
周囲辺長も高さにあたる箇所のみ記載されるだけなので、間口の記載等が無いものも当然有りますので、
復元がしずらい事です。
地積測量図はその名の通り昔は土地の面積のみ算出するものであり、面を作っている線と点については、
復元力まで求めていなかったので当然その様な弱点にも目をつぶっていました。
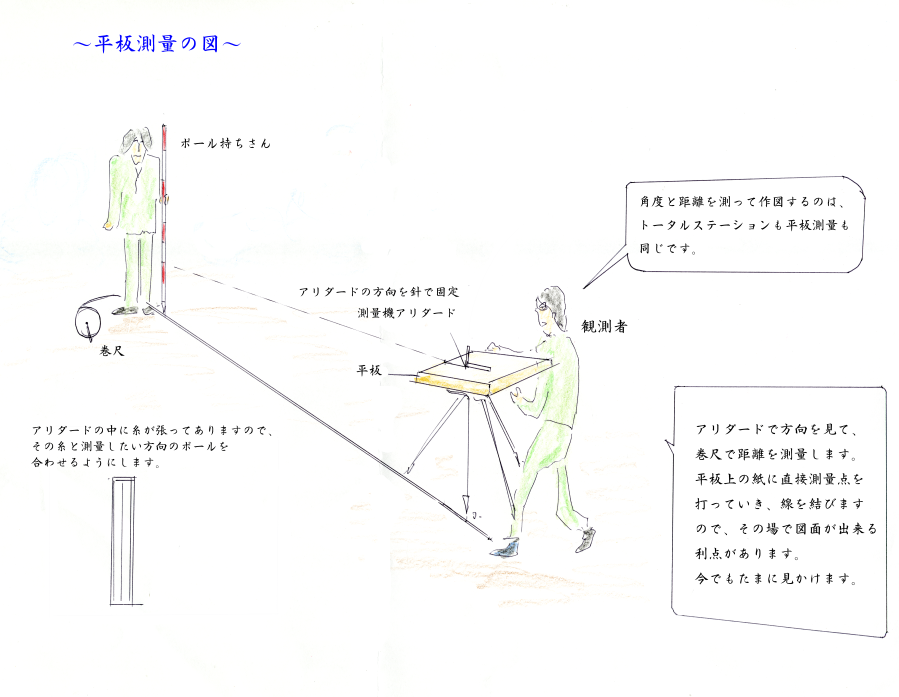
この図面の作成方法は、平板測量(別図参照)で形状を測量した土地の形状を事務所に持ち帰って机上で
三角形に分けて三角スケールで底辺と高さを読んでその読んだ長さで三角形の計算をしました。
よって1/250の縮尺のものより1/100の縮尺のものの方がスケールで読み易くなる分だけ精度が良くなる筈です。
土地境界線を復元する時は後から読んだ数値で復元するよりも、平板測量の成果の土地形状の方が正しい訳
ですからスキャナで読み込んでデータ化したものを動いていなさそうな境界点2点から張り合わせた方が
精度の良い復元になると考えられます。
又、わざわざ必須記載事項で無い周囲の辺長を記載している場合もありますが、その辺長は巻尺で実測した
ものと考えられますので、追いかける基準ポイントを間違えなければ採用して良い数値と思われます。
当時から実測出来そうな箇所は、場合によっては採用しても良いと思われます。
昭和から平成の最初の頃まで使用されており、三斜といってもトータルステーション測量のものは測量
そのものの精度が良いですし、一番大事なのは、CADソフトで三斜求積をしている場合だと三角スケールで
眼で読むのでは無く、座標計算したポイントをコンピュータの計算上で底辺と高さを割りだして計算しますので、
その数値についてもかなり信憑性が有るという事です。