
1. 地図の種類 ~球体を平面にする事による誤差~

1. 地図の種類 ~球体を平面にする事による誤差~
私たちが普段使用している地図にも種類があります。 地球は球体ですのでそれを平面である地図に直す時に何を優先するかで地図の態様が変わってくるのです。
メルカトル図法は、簡単に言うと角度を優先させて形状には目をつぶっています。
モルワイデ図法は、地図上の任意の場所で実際の面積との比が等しくなりますが、縦横に比率が実際の比率と相違し、1対2となります。
グード図法は、良いところを混ぜて作成されている様です。
地球儀以外では、この様に何らかの工夫をしなければ、球面を平面に表現する事は出来ません。
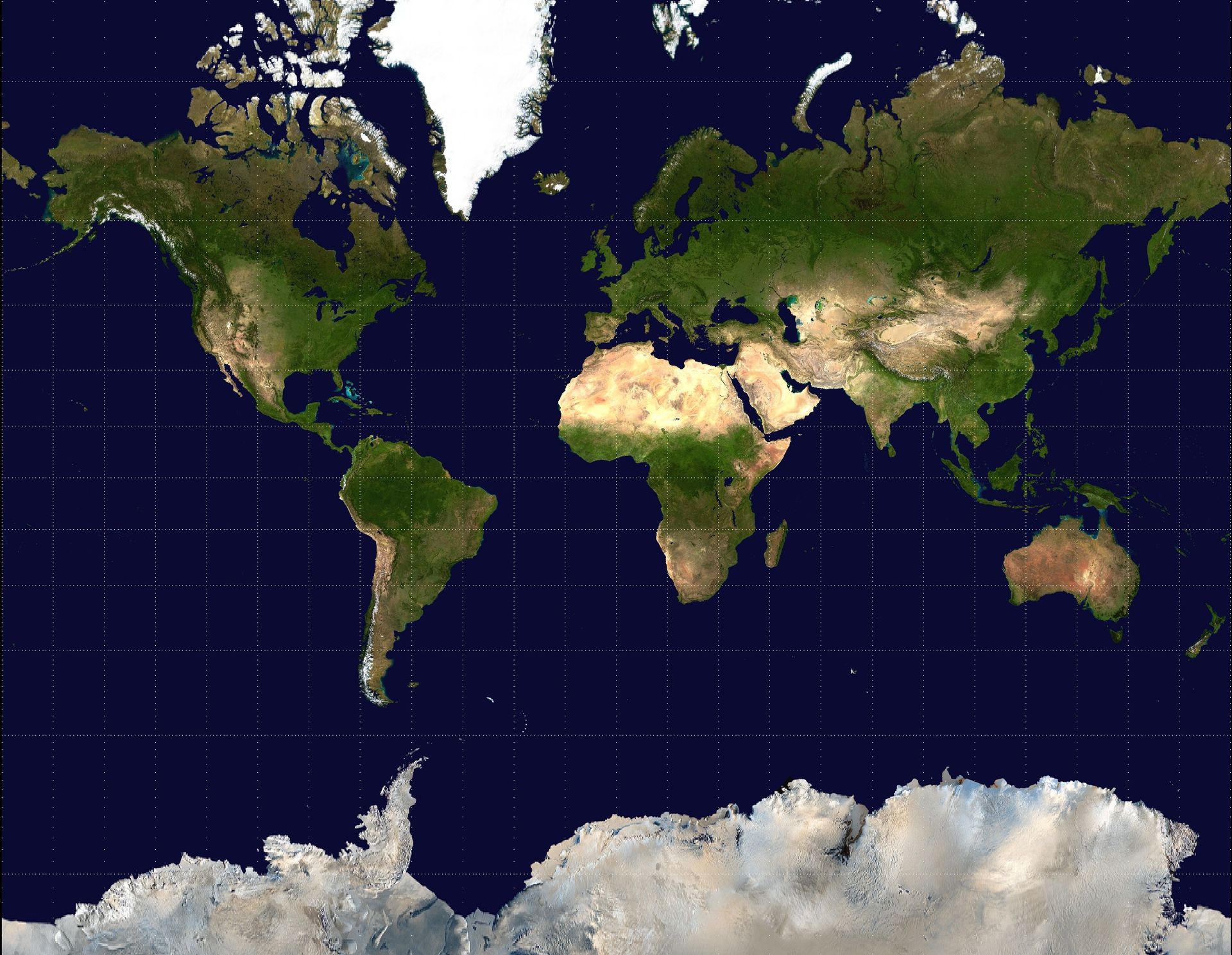
メルカトル図法(メルカトルずほう)は、1569年にフランドル(現ベルギー)出身の地理学者ゲラルドゥス・メルカトルがデュースブルク(現ドイツ)で発表した地図に使われた投影法である。図の性質と作成方法から正角円筒図法ともいう。等角航路が直線で表されるため、海図・航路用地図として使われてきた。メルカトルが発案者というわけではなく、ドイツのエアハルト・エッツラウプが1511年に作成した地図にはすでに使われていた。
この図法は地球儀を円筒に投影したもので、地軸と円筒の芯を一致させ投影するため経線は平行直線に、緯線は経線に直交する平行直線になる。ところで正角性を維持するには、横方向・縦方向の拡大率を一致させる必要がある。緯線はすべて赤道と同じ長さになるので、高緯度地方に向かうにつれて実際の長さ(地球儀上の長さ)より横方向に拡大される。それに応じて縦方向(経線方向)にも拡大させるので、高緯度に向かうにつれ距離や面積が拡大されることになる。例えば緯度60度では、本来の緯線の長さは赤道の半分なので2倍に拡大され、したがって経線も2倍に拡大されるので、面積は4倍に拡大される。より高緯度のグリーンランドの面積は実際より17倍も拡大されている。
メルカトル図法の地図において、出発地と目的地との間に直線を引いて経線となす角度(「舵角」と言う)を測り、方位磁針を見ながら常にその角度へ進むようにすれば、
(北磁極と真北の差を誤差として)目的地に到着する。このコースは航程線(等角航路)と呼ばれ、多くの場合に最短距離(大圏コース)から大きく外れるが、舵取りが容易なため
羅針盤が発明された時代から広く利用されてきた。なお航程線が直線になるのは経線が平行直線であり、正角図法だからである。
メルカトル図法の大きな特徴は角度が正しい、すなわち十分狭い範囲だけを見ると形が正しい事である。一方で緯度によって縮尺が変化し、特に高緯度地方は著しく
拡大されてしまう。そのため、広い範囲での角度、距離、面積比は正しくない。また極においては、極も赤道と同じ長さで表現されるので横方向に無限大に拡大され、
正角性を維持するため縦方向も無限大に拡大しなければならない。これは実際には不可能なので、極を表現できない。よってメルカトル図法では原理的に世界全図を描けない。そこで高緯度地方が拡大しないよう、経線方向の伸びを圧縮したのがミラー図法である。世界全図が表現できるようになったが、正角性は失われている。
近年では、ネット上におけるシームレスな世界地図の表現方法として、メルカトル図法が用いられている。北が必ず上であり、正角図法であるため十分拡大すれば歪みが
問題とならない。実際には、縮尺ごとに巨大なメルカトル図法の世界地図画像を用意し、要求された範囲だけを四角く切り抜いて送り出せばよい。ただし縮尺は緯度によって変わるので、
比較のための尺を変化させる必要がある。
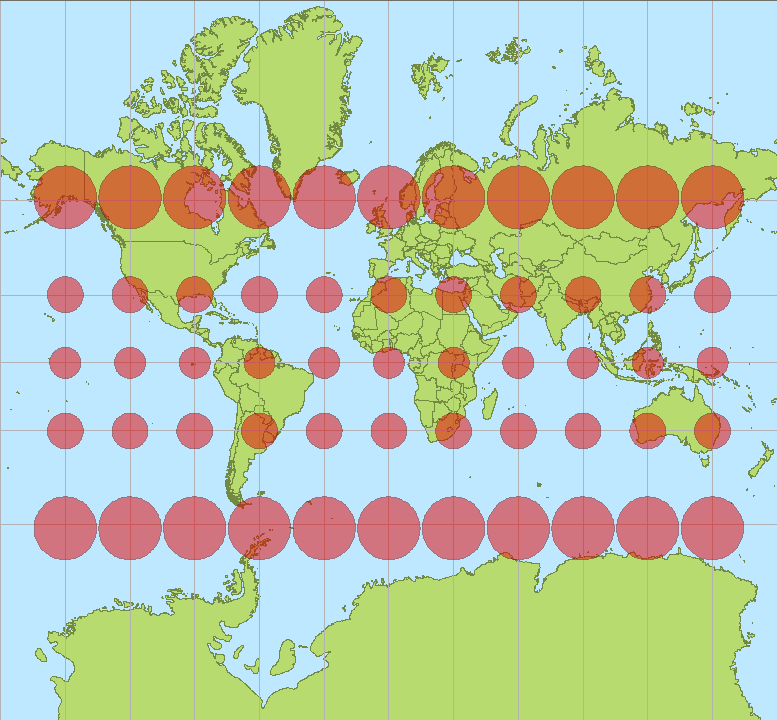
赤い円(テイソーの指示楕円)は、地球上の同じ大きさの円をメルカトル図法で投影したもの。どの円も小さければ歪む事なく円になるが、大きさは緯度によって異なる
モルワイデ図法(モルワイデずほう)は、1805年にドイツの天文学者・数学者カール・モルワイデが考案した地図投影法の一種である。
擬円筒図法の一種で、地図上の任意の場所で実際の面積との比が等しくなる正積図法である。地球全体を1枚の平面に表現でき、地図の外周は楕円形になる。楕円の
長径(横)と短径(縦)の比は2:1となり、もし縮尺1分の1の地図を作成したとすれば、横36040km、縦18020kmの楕円となる。
緯線はどれも水平な直線になる。経線は中央経線が垂直な直線となるが、それ以外の経線は弧を描く。等積になるように緯線の間隔を調整するため、距離の比は一定に
なっていない。赤道上では正角でなく、南北方向が東西方向に比べ1.234倍伸びている。中央経線上で正角になるのは緯度40度44分である[1]。地図の周辺部の歪みが
大きくなるが、サンソン図法ほど大きくはない。
主に分布図に利用される。
フランス地理学の祖と言われるニコラ・サンソン(Nicolas Sanson、1600 - 1667年)が、1650年発行の地図帳に用いたことからこの名前がついている。
しかし16世紀からゲラルドゥス・メルカトルはじめ幾つかの地図帳に用いられていて、実際の考案者は分かっていない。経線が正弦曲線(サインカーブ)で
表されることから正弦曲線図法 (sinusoidal projection) とも呼ばれる。また、イギリスの天文学者ジョン・フラムスティード (John Flamsteed) が星図に用いたことから
サンソン=フラムスティード図法、また上記メルカトルの地図帳からサンソン=メルカトル図法などの名前で呼ばれることもある。
擬円筒図法に分類される。また、地図上の任意の場所で実際の面積との比が等しくなる正積図法である。正軸の場合、赤道上と中央経線(曲線ではなく直線で表される経線)上
での距離の比が等しい。
同じ正積・擬円筒図法のモルワイデ図法と比較されることが多い。サンソン図法では赤道付近と中央経線付近は正しい形で表されるのに対し、
モルワイデ図法では赤道付近が縦方向に伸び、中央経線上では距離の比と縦横の比が緯度によって変化する。またサンソン図法では、
赤道だけでなく他の緯線でも緯線上だけに限れば赤道上と同じ距離の比である。しかし中央経線から離れた中高緯度帯では、外周の正弦曲線の形に合わせて斜めに大きく歪む。
また極部分では(経線が楕円として表されるモルワイデ図法と違い)経線が直線的に集まるため、歪みが大きくなり正しい形で表されない。
地球全体を表す主題図としては適さないが、他の図法に比べて計算が容易である。
グード図法(グードずほう)、ホモロサイン図法(ホモロサインずほう)、あるいは断裂ホモロサイン図法(だんれつホモロサインずほう)は、
断裂のある投影法で、擬円筒図法かつ正積図法である。複数の図法を合成した図法で、世界地図に使われている。世界規模で面積の関係を表示する目的で、メルカトル図法の代替図法としてジョン・ポール・グードが1923年に考案した
投射図は12個の領域からなり、6個の断裂片を含む。高緯度地方の6領域をモルワイデ図法で表現し、低緯度地方のサンソン図法と接続する
。「ホモロサイン」とは「ホモログラフ図法」(モルワイデ図法)と「シヌソイダル図法」(正弦曲線図法)の合成語で、グードによって名づけられた。
モルワイデ図法とサンソン図法の結合箇所は、同じ面積縮尺の両図法において、緯線長が一致する北緯(または南緯)40度44分であり、
この緯度で地図の縁が僅かに折れ曲がっている。結合した両図法がどちらも正積図法のため、この図法も正積図法になる。